Công thức tính độ dài đường trung tuyến là tài liêu vô nằm trong hữu ích tuy nhiên Download.vn ham muốn ra mắt cho tới quý thầy cô với những em lớp 10 tham khảo.
Tài liệu tổ hợp toàn cỗ kỹ năng và kiến thức về đàng trung tuyến là gì, đặc thù đàng trung tuyến vô tam giác, công thức tính đàng trung tuyến và những dạng bài bác tất nhiên. Qua cơ canh ty những em học viên nhanh gọn nắm rõ kỹ năng và kiến thức nhằm giải nhanh chóng những bài bác Toán 10.
Bạn đang xem: Công thức đường trung tuyến chi tiết nhất
1. Đường trung tuyến là gì?
- Đường trung tuyến của một quãng trực tiếp là 1 đường thẳng liền mạch trải qua trung điểm của đoạn trực tiếp cơ.
2. Đường trung tuyến của tam giác
- Đường trung tuyến của một tam giác là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập vô hình học tập phẳng phiu. Mỗi tam giác với 3 đàng trung tuyến.
3. Tính hóa học đàng trung tuyến vô tam giác
- Ba đàng trung tuyến của tam giác nằm trong trải qua một điểm. Điểm cơ cơ hội đỉnh một khoảng chừng vày 2/3 độ dài đường trung tuyến trải qua đỉnh ấy.
Giao điểm của phụ vương đàng trung tuyến gọi là trọng tâm.
Ví dụ:
Gọi G là trọng tâm của tam giác ABC, ABC với những trung tuyến AI, BM, công nhân thì tớ sẽ có được biểu thức:
Đường trung tuyến vô tam giác vuông
- Tam giác vuông là 1 tình huống đặc trưng của tam giác, vô cơ, tam giác sẽ có được một góc có tính rộng lớn là 90 phỏng, và nhị cạnh tạo ra góc này vuông góc cùng nhau.
- Do cơ, đàng trung tuyến của tam giác vuông sẽ có được không thiếu những đặc thù của một đàng trung tuyến tam giác.
Định lý 1: Trong một tam giác vuông, đàng trung tuyến ứng với cạnh huyền vày nửa cạnh huyền.
Định lý 2: Một tam giác với trung tuyến ứng với cùng một cạnh vày nửa cạnh cơ thì tam giác ấy là tam giác vuông.
Ví dụ:
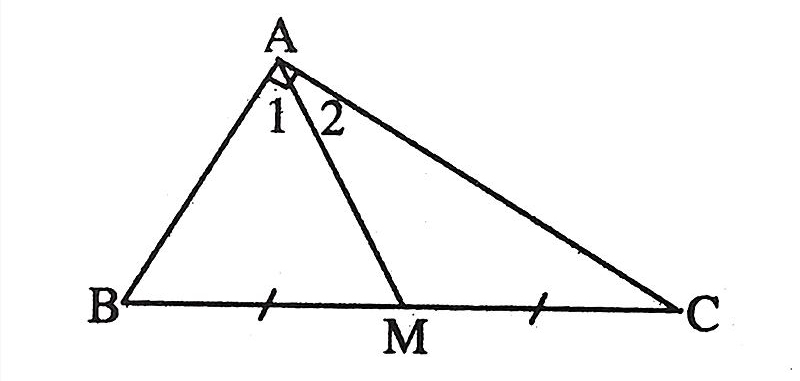
Tam giác ABC vuông ở A, độ dài đường trung tuyến AM tiếp tục vày MB, MC và vày 50% BC
Ngược lại nếu như AM = 50% BC thì tam giác ABC tiếp tục vuông ở A.
4. Công thức đàng trung tuyến
Trong đó: a, b ,c thứu tự là những cạnh vô tam giác
ma, mb, mc chuyến lượt là những đàng trung tuyến vô tam giác
5. Bài luyện về phong thái tính độ dài đường trung tuyến
Bài 1: Cho tam giác ABC cân nặng ở A có AB = AC = 17cm, BC= 16cm. Kẻ trung tuyến AM.
a) Chứng minh: AM ⊥ BC;
b) Tính độ dài AM.
Hướng dẫn giải
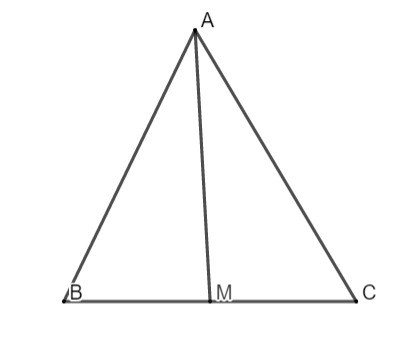
a. Ta với AM là đàng trung tuyến tam giác ABC nên MB = MC
Mặt không giống tam giác ABC là tam giác cân nặng bên trên A
Suy rời khỏi AM một vừa hai phải là đàng trung tuyến một vừa hai phải là đàng cao
Vậy AM vuông góc với BC
b. Ta có
BC = 16cm nên BM = MC = 8cm
AB = AC = 17cm
Xét tam giác AMC vuông bên trên M
Áp dụng quyết định lý Pitago tớ có:
AC2 = AM2 + MC2 ⇒ 172 = AM2 + 82 ⇒ AM2 = 172 - 82 = 225 ⇒ AM = 15cm
Bài 2: Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng GA = GB = GC.
Hướng dẫn giải
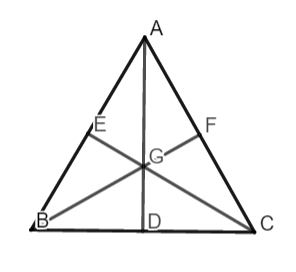
Gọi AD, CE, BF là những đàng trung tuyến tam giác ABC hoặc D, E, F thứu tự là trung điểm cạnh BC, AB, AC
Ta với AD là đàng trung tuyến tam giác ABC nên (1)
CE là đàng trung tuyến tam giác ABC nên (2)
BF là đàng trung tuyến tam giác ABC nên (3)
Ta với tam giác BAC đều nên đơn giản và dễ dàng suy rời khỏi AD = BF = CE (4)
Từ 1, 2, 3, 4 suy rời khỏi AG = BG = CG
Bài 3: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho tới AD = AB. Trên cạnh AC lấy điểm E sao cho tới AE = 1/3AC. Tia BE rời CD ở M. Chứng minh :
Xem thêm: Vệ Sinh Máy Lạnh Tại Nhà Giá Rẻ - Có Mặt Sau 30 Phút
a) M là trung điểm của CD
b) AM = BC.
Hướng dẫn giải
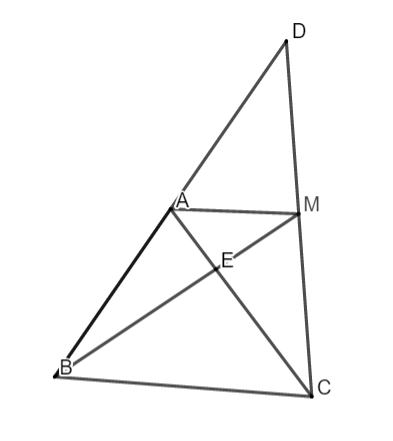
a. Xét tam giác BDC với AB = AD suy rời khỏi AC là đàng trung tuyến tam giác BCD
Mặt khác
Suy rời khỏi E là trọng tâm tam giác BCD
M là uỷ thác của BE và CD
Vậy BM là trung tuyến tam giác BCD
Vậy M là trung điểm của CD
b. A là trung điểm của BD
M là trung điểm của DC
Suy rời khỏi AM là đàng tầm của tam giác BDC
Suy rời khỏi AM = 50% BC
Bài 4: Cho tam giác ABC, trung tuyến BM. Trên tia BM lấy nhị điểm G và K sao cho tới BG = BM và G là trung điểm của BK. Gọi N là trung điểm của KC , GN rời CM ở O. Chứng minh:
a) O là trọng tâm của tam giác GKC ;
b) GO = BC
Học sinh tự động giải
Bài 5: Cho tam giác ABC vuông ở A, với AB = 18cm, AC = 24cm. Tính tổng những khoảng cách kể từ trọng tâm G của tam giác cho tới những đỉnh của tam giác.
Hướng dẫn giải
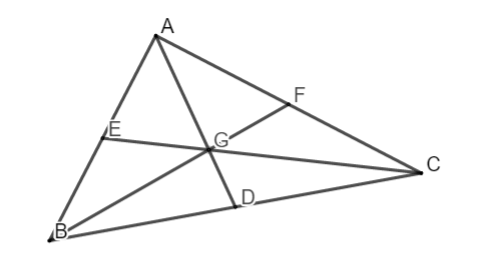
Gọi AD, CE, BF thứu tự là những đàng trung tuyến nối kể từ đỉnh A, C, B của tam giác ABC
Dễ dàng suy rời khỏi AE = EB = 9cm, AF = FC = 12cm
Ta với tam giác ABC vuông bên trên A, vận dụng quyết định lý Pitago tớ có:
BC2 = AB2 + AC2 ⇒ BC2 = 182 + 242 = 900 ⇒ BC = 30cm
Ta với ABC vuông tuy nhiên D là trung điểm cạnh huyền nên AD = BD = DC = 15cm
Suy ra: AG = 2/3 AD = 10cm
Xét tam giác AEC vuông bên trên A, vận dụng quyết định lý Pitago tớ có:
EC2 = AE2 + AC2 ⇒ EC2 = 92 + 242 = 657 ⇒ EC = 3√73 centimet ⇒ CG = 2/3 EC = 2√73 cm
Tương tự động tớ xét tam giác AFB vuông bên trên A, vận dụng quyết định lý Pitago tớ có:
BF2 = AB2 + AF2 ⇒BF2 = 182 + 122 = 468 ⇒ BF = 6√13 centimet ⇒ BG = 2/3 BF = 4√13 cm
Tổng những khoảng cách kể từ trọng tâm G của tam giác cho tới những đỉnh của tam giác là:
AG + BG + CG = 10 + 4√13 + 2√73 (cm)
Bài 6: Cho tam giác ABC, trung tuyến AM. hiểu AM = BC. Chứng minh rằng tam giác ABC vuông ở A.
Học sinh tự động giải
Bài 7: Cho tam giác ABC. Các đàng trung tuyến BD và CE. Chứng minh
Hướng dẫn giải
Học sinh tự động vẽ hình.
Xét tam giác BGC có:
BG + CG > BC
⇒
Xem thêm: Cách tải tất cả hình ảnh từ Google Photos về máy tính
⇒ BD + CE >
....................
Mời chúng ta chuyên chở File tư liệu nhằm coi tăng nội dung chi tiết