Tính chất của trọng tâm và cách xác định trọng tâm tam giác trong Hình học

Tính hóa học của trọng tâm và cơ hội xác lập trọng tâm vô Hình học

Như chúng ta tiếp tục biết giao phó điểm của tía đàng trung tuyến vô một tam giác đó là trọng tâm của tam giác cơ, vậy bọn chúng là vấn đề thế nào và với những đặc thù quan trọng gì. Hãy nằm trong công ty chúng tôi mò mẫm hiểu nhé!

Bạn đang xem: Tính chất của trọng tâm và cách xác định trọng tâm tam giác trong Hình học

I. Lý thuyết về trọng tâm

    1. Trọng tâm là gì?

Trọng tâm vô tam giác là giao phó điểm của tía đàng trung tuyến xuất phát điểm từ tía đỉnh.

Cho tam giác ABC, vô cơ AM, BN, CP thứu tự là trung tuyến của tam giác xuất phát điểm từ đỉnh A, B, C. AM, BN, CP hạn chế nhau bên trên G nên G đó là trọng tâm của tam giác

Công thức liên quan:

•  Hình nhiều giác đều n cạnh
•  Hình lục giác

    2. Tính hóa học trọng tâm của tam giác

Để xác lập trọng tâm của một tam giác tao thực hiện:

Cách 1:

• Tìm trung điểm M của BC sao mang lại MC = MB
• Nối A với M ta được đàng trung tuyến AM.
• Tương tự động với những đàng trung tuyến còn lại.
• Giao 3 đàng trung tuyến là điểm G. Suy rời khỏi G chính là trọng tâm tam giác ABC.

Cách 2:

• Tìm trung điểm M của BC sao mang lại MC = MB
• Nối A với M ta được đàng trung tuyến AM.
• Trên đoạn trực tiếp AM lấy điểm G sao cho: \(AG=\dfrac{2}{3} AM\)
• Vậy theo đuổi đặc thù trọng tâm tao với G đó là trọng tâm tam giác ABC.

Cho tam giác ABC với AM, BN, CP lần lượt là tía đàng trung tuyến tại đỉnh A, B, C. Ta với giao phó của tía đàng trung tuyến là điểm G. Vậy G là trọng tâm của tam giác ABC.

Ta với tính chất:

\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM} \Rightarrow AG=\dfrac{2}{3} AM\)

\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)

II. Trọng tâm của những hình học tập quánh biệt

• Trọng tâm tam giác vuông

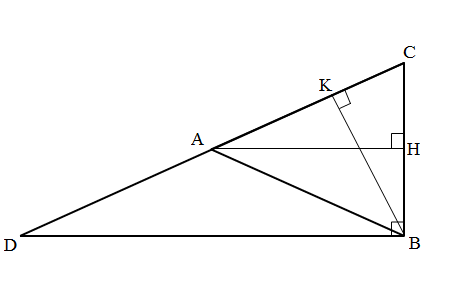
Tam giác ABC vuông bên trên B, kể từ B vẽ đàng trung tuyến BA, vì như thế BA là đàng trung tuyến của góc vuông nên: BA = một nửa CD=AD = AC.

Vậy tam giác ADB và tam giaisc ABC thứu tự cân nặng bên trên A,

• Trọng tâm tam giác cân

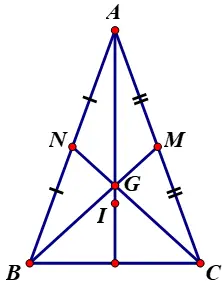
Cho tam giác ABc cân nặng bên trên A, G là trọng tâm tam giác ABC. Vì tam giác cân nặng bên trên A, nên AG một vừa hai phải là đàng trung tuyến, một vừa hai phải là đàng cao và là đàng phân giác cùa tam giác ABC.

Hệ quả:

- \(\widehat{BAG}=\widehat {CAG}\)

- AG vuông góc với BC.

Xem thêm: Đổi vé máy bay Vietnam Airlines: điều kiện, chi phí?

• Trọng tâm tam giác đều là gì

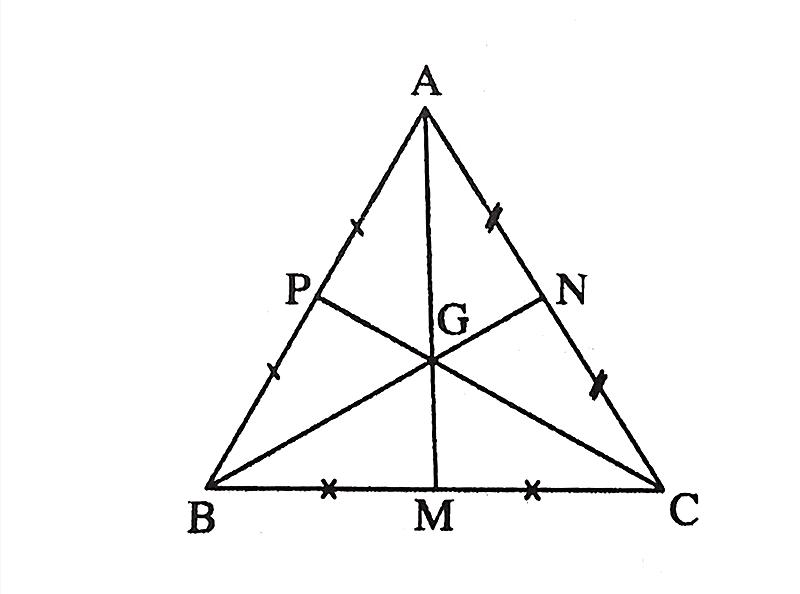
Cho tam giác ABC đều, G là giao phó điểm tía đàng trung tuyến. Theo đặc thù của tam giác đều tao với G một vừa hai phải là trọng tâm, trựa tâm, tâm đàng tròn trĩnh nước ngoài tiếp và nội tiếp của tam giác ABC.

• Trọng tâm tứ diện

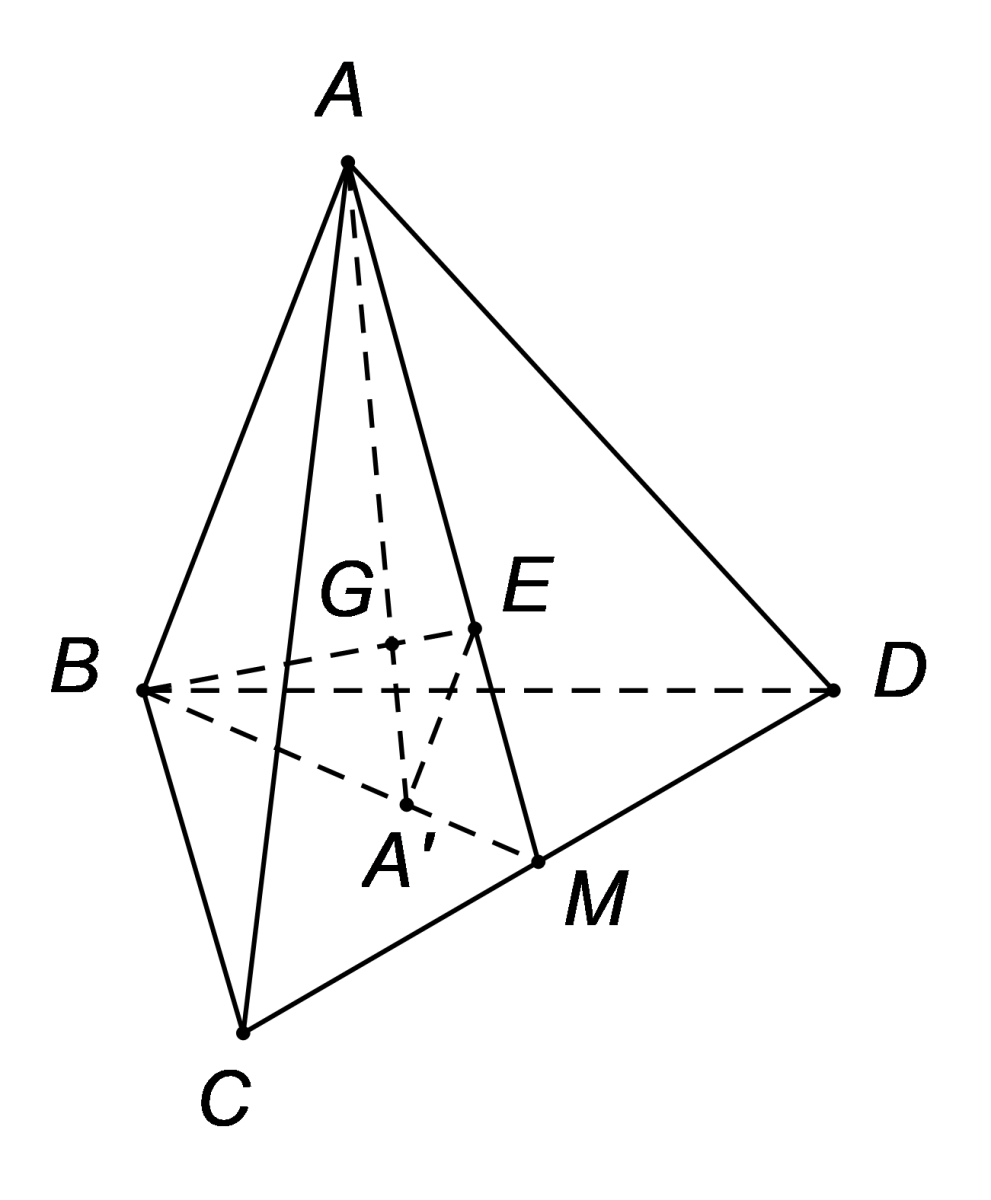
Ta với G là trọng tâm tứ diện ABCD.

Trọng tâm tứ diện là giao phó điểm của tư đường thẳng liền mạch nối đỉnh và trọng tâm của tam giác đối lập.

III. Luyện tập

Bài tập: Cho tam giác ABC, trung tuyến BM = công nhân. BM hạn chế công nhân bên trên G. CHứng minh tam giác ABC cân nặng bên trên A

Lời giải:

Vì BM và công nhân là hai tuyến phố TT của tam giác tuy nhiên BM giao phó công nhân bên trên G, nên tao có:

\(\dfrac{BG}{BM}=\dfrac{CG}{CN}=\dfrac{2}{3}\)

Mà BM = công nhân nên BG = công nhân và GN = GM

Xét \(\Delta BNG \ và \ \Delta CGM\) ta có:

BG = CN

GN = GM

\(\widehat{BGN}= \widehat{CGM}\) ( 2 goc đối đỉnh)

Suy rời khỏi : \(\Delta BNG \ đồng \ dạng \ \Delta CMG\)

Suy ra: BN = CM (1)

mà M và N thứu tự là trung điểm của AB và AC (2)

Xem thêm: Vẽ Bầu Trời Mây cơ bản - Hướng dẫn dành cho người mới bắt đầu

Từ (1) và (2) tao cí AB = AC => Tam giác ABC cân nặng bên trên A( đpcm).

Tham khảo cỗ công thức cực kỳ hóa học >>>>Toàn cỗ công thức siêu thời gian nhanh Toán 12 tương đối đầy đủ nhất kể từ A - Z ôn ganh đua THPTQG

Vậy là tất cả chúng ta tiếp tục mò mẫm hiểu đoạn về định nghĩa trọng tâm. Nếu với vướng mắc và chủ ý thú vị van nài sướng lòng nhằm lại bên dưới mục bình luận nhé, công ty chúng tôi cực kỳ mong chờ có được sự góp phần từ các bạn!