Tính thể tích vật thể tròn xoay

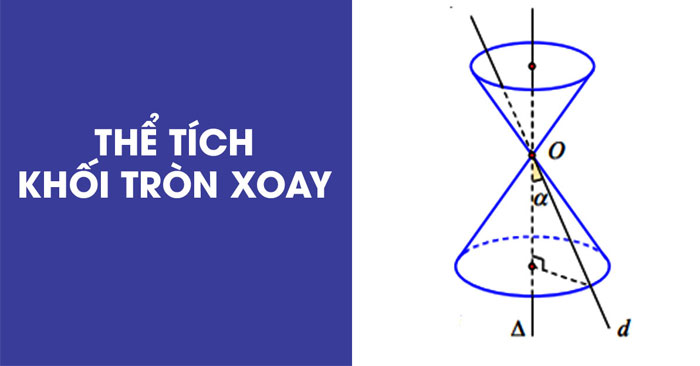
Thể tích của vật thể tròn xoe xoay được xem dựa vào công thức sau đây:
1. Trước tiên, xác lập miền (D) nhưng mà vật thể tròn xoe xoay sinh rời khỏi. Miền này được số lượng giới hạn vì thế trang bị thị của hàm số hắn = f(x), đoạn trực tiếp x = a, x = b và trục Ox.
2. Tính diện tích S S cù xung xung quanh trục Ox của phần diện tích S số lượng giới hạn D này. Công thức tính diện tích S S là: S = ∫[a,b] (π[f(x)]^2)dx.
3. Cuối nằm trong, tính thể tích V của vật thể tròn xoe xoay bằng phương pháp nhân diện tích S S tiếp tục tính được với chiều lâu năm L của vòng tròn xoe xung quanh trục Ox. Công thức tính thể tích V là: V = S * L.
Với việc vận dụng công thức này, chúng ta có thể tính được thể tích của vật thể tròn xoe xoay một cơ hội cụ thể và đúng chuẩn.

Miền số lượng giới hạn vật thể tròn xoe xoay khi tính thể tích là miền D, nhưng mà miền D được số lượng giới hạn vì thế trang bị thị của hàm số hắn = f(x), đường thẳng liền mạch x = a, đường thẳng liền mạch x = b và đường thẳng liền mạch hắn = 0.

Để tính thể tích vật thể tròn xoe xoay, tao cần thiết thực hiện công việc sau đây:
Bước 1: Xác tấp tểnh miền số lượng giới hạn của vật thể. Miền này được xác lập vì thế phương trình lối cong hoặc hàm số nhưng mà vật thể xoay xung quanh.
Bước 2: Xác tấp tểnh đoạn trực tiếp Ox nhưng mà vật thể xoay quanh. Đây là trục đối xứng của vật thể.
Bước 3: Tính diện tích S S của miền số lượng giới hạn xung xung quanh trục Ox. Đây là diện tích S của hình được dẫn đến khi miền số lượng giới hạn xoay quanh trục Ox.
Bước 4: Sử dụng công thức tính thể tích vật thể tròn xoe xoay: V = π∫(S)dx. Trong số đó, π là số Pi và ∫(S)dx là quy tắc tích phân xác lập của diện tích S S theo đòi trục x.
Bước 5: Tiến hành đo lường quy tắc tích phân nhằm xác lập độ quý hiếm thể tích V của vật thể tròn xoe xoay.
Với công việc bên trên, tao rất có thể tính được thể tích vật thể tròn xoe xoay.

Vật thể tròn xoe xoay là một trong vật thể hình không khí được tạo thành bằng phương pháp cù một hình bình hành hoặc hình mặt mày phẳng lì xung xung quanh một trục và thành quả là một trong hình thể với hình dạng tròn xoe xoay ứng.
Để tính thể tích của vật thể tròn xoe xoay, tao dùng công thức sau:
V = ∫(A)dx hoặc V = ∫(A)dy
Trong đó:
- V là thể tích của vật thể tròn xoe xoay.
- ∫ là dấu vết phân, biểu thị quy trình đo lường diện tích S A theo đòi trở thành x hoặc hắn.
- A là diện tích S hình bình hành hoặc hình mặt mày phẳng lì cù được xây cất vì thế vật thể tròn xoe xoay bên trên từng độ quý hiếm của trở thành x hoặc hắn.
Để xác lập biên phỏng của trở thành x hoặc hắn vô công thức tính thể tích, tao hay được sử dụng những điểm đỉnh của hình bình hành hoặc hình mặt mày phẳng lì cù. Các độ quý hiếm này thông thường được xác lập bằng phương pháp giải phương trình tương quan cho tới hình bình hành hoặc hình mặt mày phẳng lì.
Các công thức tính thể tích của những hình bình hành thông thường không giống nhau tùy nằm trong vô hình dạng của từng vật thể tròn xoe xoay rõ ràng. Việc đo lường diện tích S A và tiến hành quy trình tích phân rất có thể được tiến hành vì thế những cách thức như tích phân xác lập hoặc cách thức lượng giác.
Tóm lại, vật thể tròn xoe xoay là một trong vật thể được tạo nên trở nên bằng phương pháp cù một hình bình hành hoặc hình mặt mày phẳng lì xung xung quanh một trục. Thể tích của vật thể tròn xoe xoay được xem trải qua việc tích phân diện tích S của hình bình hành hoặc hình mặt mày phẳng lì cù theo đòi trở thành x hoặc hắn.

Xem thêm: Kinh nghiệm mở đại lý vé số - Hướng dẫn thủ tục, hồ sơ, kinh nghiệm

Điều khiếu nại cần thiết nhằm vận dụng công thức tính thể tích vật thể tròn xoe xoay là vật thể bại cần được tạo nên trở nên vì thế việc xoay quanh một trục cố định và thắt chặt. Nghĩa là vật thể này cần với cùng 1 lối cong đánh giá cố định và thắt chặt và xoay xung quanh một trục, tạo nên trở nên một hình dạng tròn xoe xoay.
Cụ thể, nhằm vận dụng công thức tính thể tích vật thể tròn xoe xoay, tất cả chúng ta cần thiết những vấn đề sau:
1. Đường cong đánh giá của vật thể: Đường cong này rất có thể được xác lập vì thế một hàm số hắn = f(x) hoặc x = g(y), vô bại f(x) và g(y) là những hàm số liên tiếp bên trên đoạn [a, b] với a b.
2. Đoạn [a, b]: Nó xác lập phạm vi xác lập của hàm số vô công thức đo lường.
3. Trục quay: Đường trực tiếp Ox hoặc Oy thay mặt mang đến trục cố định và thắt chặt nhưng mà vật thể xoay quanh.
Tổng hợp ý lại, nhằm tính thể tích vật thể tròn xoe xoay, tao cần thiết xác lập được lối cong đánh giá của vật thể, phạm vi xác lập của lối cong và trục cố định và thắt chặt nhưng mà vật thể xoay quanh. Sau bại, vận dụng công thức tính thể tích của vật thể tròn xoe xoay dựa vào hàm số lối cong và phạm vi xác lập nhằm đo lường thể tích ước muốn.

Việc biết công thức tính thể tích vật thể tròn xoe xoay là rất rất cần thiết vì như thế nó được cho phép tất cả chúng ta đo lường đúng chuẩn và hiệu suất cao thể tích của vật thể này. Dưới đó là nguyên nhân tại vì sao công thức này cần phải tóm vững:
1. Hiểu rõ ràng đặc thù hình học tập của vật thể: Việc biết công thức tính thể tích vật thể tròn xoe xoay sẽ hỗ trợ tất cả chúng ta nắm rõ rộng lớn về đặc thù hình học tập của vật thể này. Chúng tao rất có thể hiểu rằng địa điểm của trục cù, Điểm sáng của hình dạng và độ dài rộng của vật thể. Như vậy rất rất cần thiết khi tất cả chúng ta cần thiết đo lường những thông số kỹ thuật không giống nhau của vật thể.
2. sát dụng vô những vấn đề thực tế: Công thức tính thể tích vật thể tròn xoe xoay thông thường được vận dụng trong không ít nghành, ví dụ như nghệ thuật, xây cất, kiến thiết và ngành công nghiệp. Việc nắm rõ công thức này sẽ hỗ trợ tất cả chúng ta vận dụng vô những vấn đề thực tiễn như đo lường lượng vật tư cần dùng, tính toán và đo lường một cơ hội đúng chuẩn và hiệu suất cao.
3. Thể hiện nay sự nắm vững và khả năng xử lý vấn đề: Khi tất cả chúng ta biết và vận dụng công thức tính thể tích vật thể tròn xoe xoay, tất cả chúng ta không những thể hiện nay được kỹ năng và nắm vững về toán học tập mà còn phải đã cho thấy tài năng xử lý yếu tố, trí tuệ logic và tổ chức triển khai vấn đề một cơ hội với khối hệ thống.
Vì vậy, biết công thức tính thể tích vật thể tròn xoe xoay là rất rất cần thiết nhằm rất có thể vận dụng và phần mềm vô những vấn đề thực tiễn, tương tự thể hiện nay sự nắm vững và khả năng trong các việc xử lý yếu tố.

Có thể tính được thể tích vật thể tròn xoe xoay nhưng mà ko nên biết công thức đúng chuẩn. Dưới đó là phương pháp tính thể tích vật thể tròn xoe xoay một cơ hội đơn giản:
1. Xác tấp tểnh màn trình diễn của hàm hắn = f(x). Đây là hàm nhưng mà vật thể tròn xoe xoay được sinh vì thế khi xoay quanh trục OX.
2. Tìm khoảng tầm xác lập của x vô miền giao phó đoạn [a, b]. Như vậy canh ty xác lập vùng nhưng mà vật thể tròn xoe xoay tồn bên trên.
3. Tính diện tích S của miền số lượng giới hạn vì thế hàm f(x), trục OX và những số lượng giới hạn x = a và x = b. Như vậy được tiến hành bằng phương pháp tính tích phân xác lập của hàm f(x) trong tầm [a, b].
4. Sau khi với diện tích S, tính thể tích của vật thể tròn xoe xoay bằng phương pháp dùng công thức thể tích của hình trụ, với diện tích S thực hiện hạ tầng và phỏng lâu năm là độ cao của hình trụ.
Tuy nhiên, nhằm tính được đúng chuẩn thể tích vật thể tròn xoe xoay, việc dùng công thức đúng chuẩn và cách thức đo lường như tích phân là quan trọng.

Thể tích vật thể tròn xoe xoay là một trong định nghĩa cần thiết vô toán hình không khí vì như thế nó được cho phép tất cả chúng ta đo lường và tính toán thể tích của những vật thể với hình dạng phức tạp.
1. Ứng dụng vô cơ học tập và vật lý: Thể tích vật thể tròn xoe xoay cũng rất được dùng trong số vấn đề cơ học tập và vật lý cơ. Ví dụ, khi đo lường lượng của một vật được tạo nên trở nên từ các việc xoay quanh một trục, tao nên biết thể tích của vật thể bại.
2. Khối tròn xoe xoay: Trong tình huống của khối tròn xoe xoay, thể tích là một trong định nghĩa cần thiết nhằm đo lường diện tích S mặt phẳng cắt và diện tích S mặt phẳng của hình dạng tròn xoe xoay. phẳng phiu phương pháp tính toán thể tích, tất cả chúng ta rất có thể tìm hiểu rời khỏi diện tích S hành trình của những điểm bên trên mặt phẳng của vật thể khi nó xoay quanh một trục với vận tốc xác lập.
3. Chế phỏng ngẫu nhiên và xã hội: Tính toán và tính toán thể tích của vật thể tròn xoe xoay cũng rất được dùng trong không ít nghành không giống nhau như phong cách thiết kế, đo lường, kiến thiết, ngành công nghiệp và nhiều nghành xã hội không giống. Kiến thức về thể tích canh ty tất cả chúng ta hiểu và vận dụng những cách thức của toán học tập vô thực tiễn.
Tóm lại, thể tích vật thể tròn xoe xoay cần thiết vô toán hình không khí cũng chính vì nó cung ứng những vấn đề hữu ích và với phần mềm thoáng rộng trong số nghành không giống nhau.

Xem thêm: Câu hỏi tự luận mức độ thông hiểu Ngữ văn 11 kết nối bài 4: Thuyền và biển (Xuân Quỳnh)

Thể tích vật thể tròn xoe xoay được dùng và phần mềm trong không ít nghành không giống nhau, bao gồm:
1. Toán học: Tính thể tích vật thể tròn xoe xoay là một trong vấn đề cơ phiên bản vô toán hình không khí lớp 12. Đối tượng của vấn đề này là vật thể được tạo nên trở nên vì thế việc xoay quanh một lối cong xác lập. Bài toán này canh ty học viên nắm rõ kỹ năng về diện tích S và thể tích hình cầu, hình trụ, hoặc những hình không giống rất có thể được màn trình diễn vì thế lối cong.
2. Kỹ thuật: Trong nghành nghệ thuật, việc đo lường thể tích vật thể tròn xoe xoay rất rất cần thiết. Ví dụ, vô kiến thiết ống dẫn hoặc những khối hệ thống ống dẫn hóa học lỏng, việc đo lường thể tích của ống hoặc bể chứa chấp rất có thể trở nên tròn xoe xoay canh ty xác lập dung tích chứa chấp hóa học cần dùng.
3. Xây dựng: Trong nghành xây cất, thể tích vật thể tròn xoe xoay cũng rất được dùng nhằm đo lường những dự án công trình phong cách thiết kế tương quan cho tới hình dạng tròn xoe xoay. Ví dụ, việc đo lường thể tích của cột, xi-măng trụ, ao chứa chấp nước, hố sụt khu đất rất có thể được tổ chức dựa vào công thức tính thể tích vật thể tròn xoe xoay.
4. Thiết kế tiếp sản phẩm: Trong nghành kiến thiết thành phầm, việc đo lường thể tích vật thể tròn xoe xoay rất có thể canh ty xác lập dung tích của những thành phầm tròn xoe xoay như chai lọ, hũ đựng, ống hít, vòng bi, v.v.
Tóm lại, đo lường thể tích vật thể tròn xoe xoay với phần mềm thoáng rộng trong số nghành toán học tập, nghệ thuật, xây cất và kiến thiết thành phầm.