Đường cao của tam giác là gì? Tính chất, công thức,. bài tập

Hầu như toàn bộ đề toán nào là cũng có thể có sự xuất hiện nay của đàng cao. Vậy đàng cao của tam giác là gì? Các đặc điểm và công thức tính chừng lâu năm của đàng cao vô tam giác là gì? quý khách hàng với đầy đủ thỏa sức tự tin nhằm xác minh rằng tôi đã cầm không còn những kỹ năng và kiến thức này không? Nếu ko thì nằm trong BamBoo ôn luyện vớ tần tật qua quýt nội dung bài viết tiếp sau đây nhé!

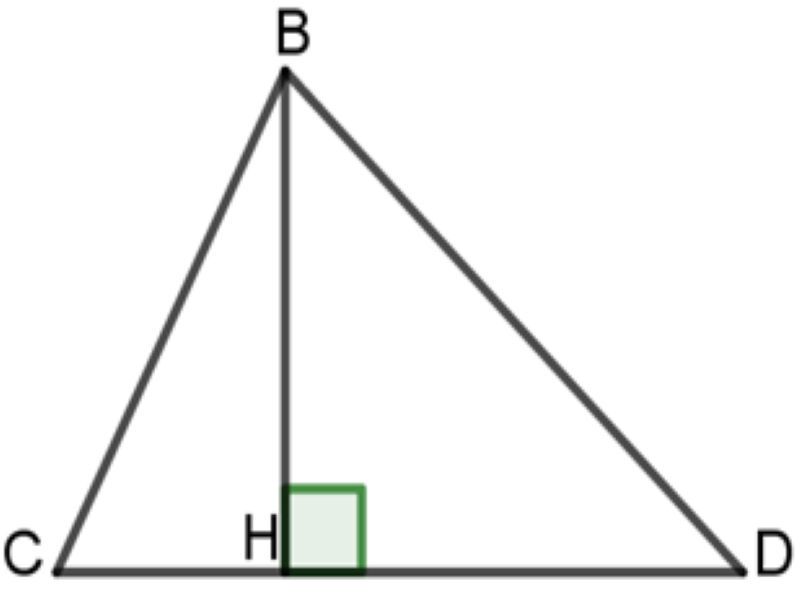
• Đường cao của tam giác là đoạn trực tiếp vuông góc được kẻ từ là 1 đỉnh cho tới đường thẳng liền mạch chứa chấp cạnh đối lập của tam giác bại.
• Cạnh đối lập được gọi là lòng ứng với đàng cao bại.
• Giao điểm thân thuộc lòng và đàng cao được gọi là chân của đàng cao.
• Độ lâu năm của đàng cao được xem vị khoảng cách kể từ đỉnh cho tới lòng.

Tìm hiểu đặc điểm đàng cao vô tam giác

Tính hóa học đàng cao vô tam giác cân

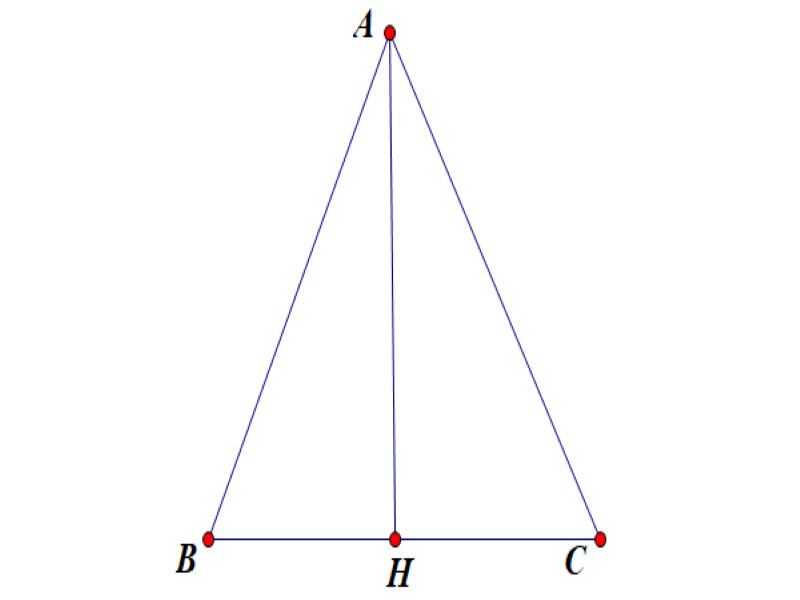
Trong tam giác cân nặng, theo dõi khái niệm, đàng cao ứng với cạnh lòng đó là đàng trung tuyến ứng với cạnh lòng bại. Như vậy, đàng cao của tam giác cân nặng trải qua trung điểm của cạnh lòng.

Bạn đang xem: Đường cao của tam giác là gì? Tính chất, công thức,. bài tập

Ngoài rời khỏi, đàng cao của tam giác cân nặng bên cạnh đó cũng chính là đàng phân giác của góc ở đỉnh và đàng trung trực của lòng tam giác. Ngược lại nếu mà một tam giác những với đàng cao bên cạnh đó cũng chính là đàng trung tuyến hoặc phân giác thì tam giác bại đó là tam giác cân nặng.

Tính hóa học đàng cao vô tam giác vuông

Trong tam giác vuông thì đàng cao với lòng là một trong những cạnh góc vuông đó là cạnh góc vuông sót lại. Như vậy thì đỉnh góc vuông đó là chân đàng cao hạ kể từ nhị đỉnh sót lại xuống nhị cạnh góc vuông của tam giác.

Tính hóa học đàng cao vô tam giác đều

Tam giác đều là một trong những dạng đặc trưng của tam giác cân nặng. Do bại, đặc điểm đàng cao vô tam giác đều cũng tương tự động như đặc điểm đàng cao vô tam giác cân nặng.

Tìm hiểu những công thức tính đàng cao vô tam giác

Công thức Heron – Công thức tổng quát lác nhằm tính chừng lâu năm đàng cao của tam giác thường

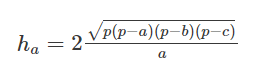
Trong đó:

• a,b,c là chừng lâu năm phụ thân cạnh của tam giác
• p là nửa chu vi: p=a+b+c2
• ha là chừng lâu năm đàng cao ứng với cạnh đáy a 

Ngoài rời khỏi, còn tồn tại những công thức tính đàng cao vô tam giác đặc trưng như tại đây.

Công thức tính đường cao trong tam giác cân

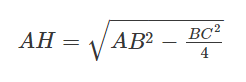
Công thức tính đàng cao vô tam giác đều

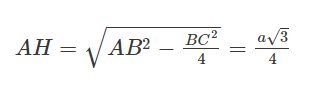
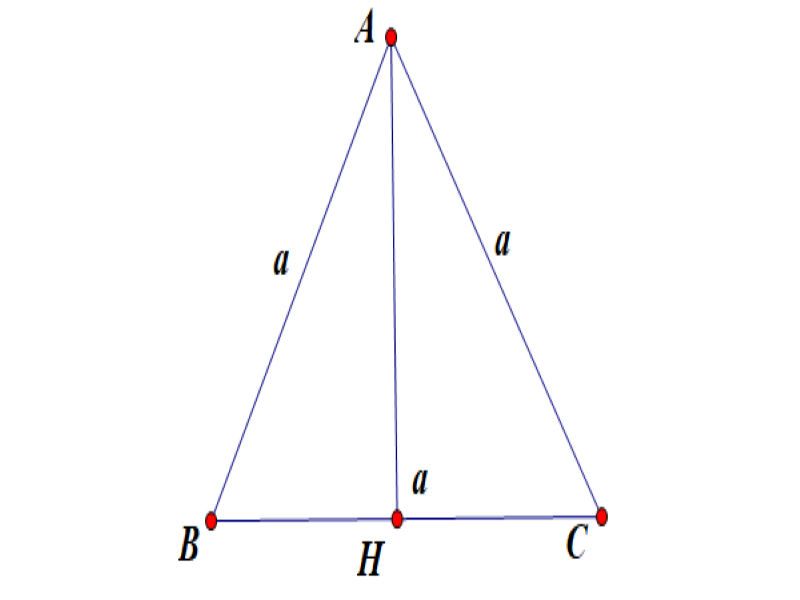
Công thức tính đàng cao vô tam giác vuông

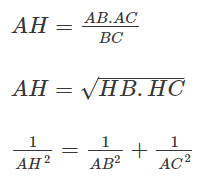
Tìm hiểu về trực tâm tam giác

Định nghĩa trực tâm là gì?

Trực tâm của tam giác hiểu giản dị và đơn giản đó là phú của phụ thân đàng cao bắt đầu từ phụ thân đỉnh của tam giác bại, bên cạnh đó vuông góc với cạnh đối lập. Ba đàng cao này tiếp tục phú nhau bên trên một điểm, tao gọi này đó là trực tâm của tam giác.

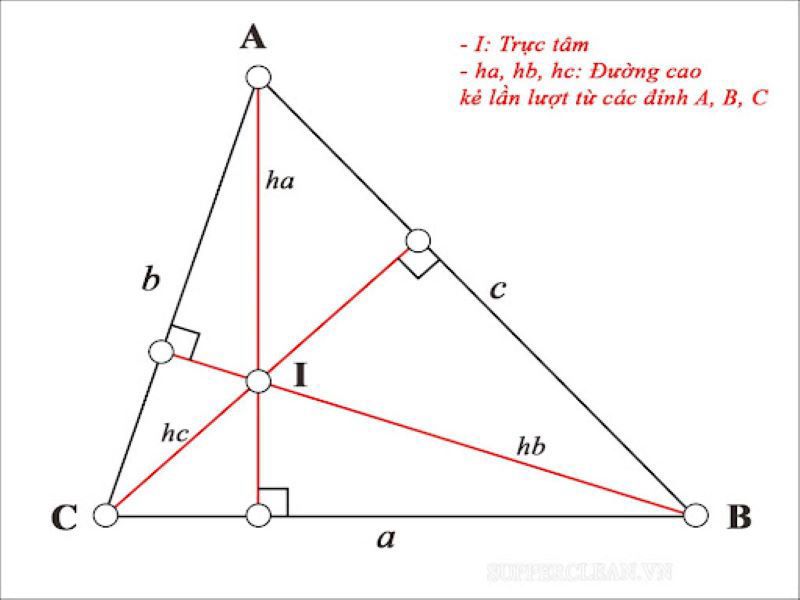
Tính hóa học trực tâm tam giác

Có 5 đặc điểm trực tâm tam giác như sau:

Xem thêm: Xuất siêu là gì? Việt Nam là nước xuất siêu hay nhập siêu?

• Trong một tam giác cân nặng thì đàng trung trực ứng với cạnh lòng tiếp tục bên cạnh đó là đàng phân giác, đàng cao và đàng trung tuyến của tam giác bại.
• Trong một tam giác, nếu mà một đàng trung tuyến bên cạnh đó là đàng phân giác thì tam giác này sẽ là tam giác cân nặng.
• Trong một tam giác, nếu mà một đàng trung tuyến bên cạnh đó là đàng trung trực thì tam giác này sẽ là tam giác cân nặng.
• Trực tâm của tam giác nhọn ABC tiếp tục trùng với tâm của đàng tròn trĩnh nội tiếp tam giác với phụ thân đỉnh là chân của phụ thân đàng cao kể từ những đỉnh A, B, C cho tới những cạnh đối diện  BC, AC, AB ứng.
• Đường cao tam giác ứng với cùng 1 đỉnh rời đàng tròn trĩnh nước ngoài tiếp tại  một điểm loại nhị được xem là đối xứng của trực tâm qua quýt cạnh ứng.

Ví dụ về tính chất chừng lâu năm đàng cao vô tam giác

Cho tam giác ABC vuông bên trên A, AB=24cm, AC=32cm. Đường trung trực của BC rời AC, BC theo dõi trật tự D và E. Tính DE?

Bài giải:

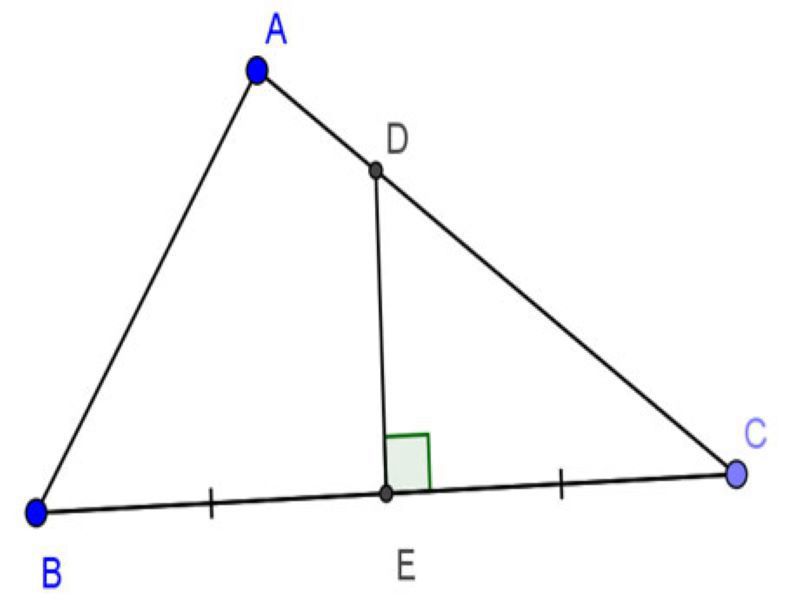
Xét tam giác vuông ABC, tao có:

BC² = AB²+ AC² ( theo dõi quyết định lý py-ta-go)

BC² = 24²+ 32²

BC² = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20(cm)

Xét tam giác vuông Ngân Hàng Á Châu và tam giác vuông ECD có:

Có ∠A = ∠E = 90o

∠C chung

=> Tam giác Ngân Hàng Á Châu ∾ tam giác ECD (g.g)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Xem thêm: Kinh nghiệm mở đại lý vé số - Hướng dẫn thủ tục, hồ sơ, kinh nghiệm

Vậy ED = 15cm

Xem thêm: 

• Khái niệm tam giác đồng dạng và những tình huống tam giác đồng dạng hoặc gặp
• Đường tròn trĩnh nội tiếp tam giác là gì? Tính hóa học và cơ hội xác lập nội tiếp tam giác
• Các tình huống cân nhau, đồng dạng của tam giác vuông và ví dụ minh họa với đáp án

Vậy bên trên đấy là những kỹ năng và kiến thức về đàng cao của tam giác tuy nhiên chắc rằng những các bạn sẽ nhớ dùng cho tới vô toàn bộ những cuộc ganh đua Toán học tập. Hy vọng nội dung bài viết này được xem là mối cung cấp xem thêm hữu ích vô quy trình tiếp thu kiến thức của chúng ta.