Cách giải phương trình bậc 2 - Học Tốt Blog

Phương trình bậc 2 là 1 trong mỗi dạng phương trình xuất hiện nay thật nhiều nhập quy trình học tập, thực hiện bài xích tập dượt hoặc cả trong những bài xích đua nhập công tác trung học cơ sở. Độ khó khăn của dạng bài xích này cũng vô nằm trong đa dạng và phong phú không giống nhau nên vẫn khiến cho vô số những em học viên bắt gặp trở ngại. Chính chính vì thế, HOCMAI tiếp tục share cơ hội giải phương trình bậc 2 nhằm những em hoàn toàn có thể cầm được những kỹ năng và kiến thức tổng quát lác nhất về dạng phương trình này.

Phương trình bậc 2 là phương trình tổng quát lác đem dạng: ax²+bx+c=0 ( điều kiện: a≠0) (1)

Bạn đang xem: Cách giải phương trình bậc 2 - Học Tốt Blog

Việc giải phương trình bậc 2 là đi kiếm toàn bộ những độ quý hiếm của x nhằm vừa lòng điều khiện khi thay cho x nhập phương trình (1) thì ax²+bx+c=0.

Để hiểu biết thêm kỹ năng và kiến thức cụ thể, những em học viên hoàn toàn có thể tìm hiểu thêm bài xích viết: Phương trình bậc 2 một ẩn

B. Phương pháp giải phương trình bậc 2

Để giải phương trình bậc 2, những em học viên cần thiết tiến hành theo gót quá trình sau:

Bước 1: Tính giá chỉ trính của Δ với Δ=b²-4ac

Bước 2: Xét tập dượt nghiệm của phương trình bằng sự việc sánh giá  Δ với 0

Δ < 0 => phương trình bậc 2 vô nghiệm
Δ = 0 => phương trình bậc 2 đem nghiệm kép x1 = x2 = -b/2a
Δ > 0 => phương trình (1) đem 2 nghiệm phân biệt, tao người sử dụng công thức nghiệm sau:

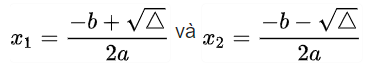
Lưu ý: Trong một vài tình huống đặc biệt quan trọng, những em học viên hoàn toàn có thể nhẩm nhanh chóng nghiệm của phương trình bậc 2

• Trong tình huống những thông số a+b+c=0 thì x1 = 1, x2 = c/a
• Trong tình huống những thông số a-b+c=0 thì x1 = -1, x2 = -c/a

Tham khảo thêm: Công thức nghiệm của phương trình bậc 2

Một số ví dụ giải phương trình bậc 2

Ví dụ 1: Giải phương trình 4x² – 2x – 6 = 0 

Ta có: Δ = (-2)² – 4.4.(-6) = 4 + 96 = 100 > 0

=> Vậy phương trình 4x² – 2x – 6 = 0  đem 2 nghiệm phân biệt.

Áp dụng công thức tao có:

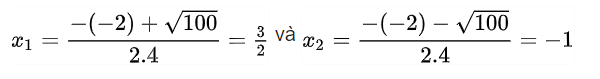
Các em học viên hoàn toàn có thể vận dụng công thức nhẩm nhanh chóng nhưng mà HOCMAI vẫn nhắc phía trên như sau:

Do a – b + c = 4 – (-2) + (-6) = 0

Vậy nghiệm của phương trình vẫn cho tới là: x1 = -1; x2 = – (-6)/4 = 3/2

Ví dụ 2: Giải phương trình 2x² – 7x + 3 = 0 

Ta đem Δ = (-7)² – 4.2.3 = 49 – 24= 25 > 0

=> Vậy phương trình 2x² – 7x + 3 = 0 đem 2 nghiệm phân biệt

Áp dụng công thức tao có:

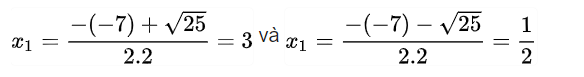
Để đánh giá 2 nghiệm bên trên vẫn đích hoặc ko, những em học viên hoàn toàn có thể thế 2 sản phẩm vừa vặn tìm kiếm được nhập phương trình bên trên.

Ví dụ 3: Giải phương trình 3x² + 2x + 5 = 0

Ta đem Δ = 2² – 4.3.5 = -56 < 0

=> Vậy phương trình 3x² + 2x + 5 = 0 là phương trình vô nghiệm.

Ví dụ 4: Giải phương trình x² – 4x +4 = 0

Ta đem Δ = (-4)² – 4.4.1 = 0

=> Vậy phương trình x² – 4x +4 = 0 đem nghiệm kép (hay phương trình đem 2 nghiệm giống như nhau)

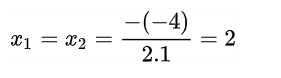
Bên cạnh bại, nhập thắc mắc này, những em học viên hoàn toàn có thể vận dụng hằng đẳng thức xứng đáng nhớ: (a-b)² = a² – 2ab + b² nên phương trình bên trên về dạng (a – 2)² = 0 => x = 2

C. Một số dạng bài xích về giải phương trình bậc 2

 Dạng 1: Bài tập dượt giải phương trình bậc 2 ko chứa chấp tham ô số

Để giải được phương trình nằm trong dạng này, cách thức phổ cập nhất là dùng công thức tính 2 đại lượng Δ hoặc Δ’, tiếp sau đó vận dụng công thức nhằm dò xét những nghiệm của phương trình.

Ví dụ 1: Giải những phương trình sau:

1. x² – 3x + 2 = 0
2. x² + x – 6 = 0

Hướng dẫn giải:

1. Ta đem Δ=(-3)² – 4 . 2 = 1.

Vậy nghiệm của phương trình là:

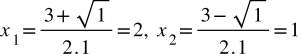
Ngoài đi ra, tao hoàn toàn có thể vận dụng cách thức tính nhanh chóng của phương tình này: tao thấy 1 + (-3) + 2 = . Vậy tao hoàn toàn có thể suy đi ra nghiệm của phương trình là x1 = 1 và x2 = 2/1 = 2

2. Ta đem Δ=1² – 4 . (-6) = 25. Vậy nghiệm của phương trình vẫn cho tới là

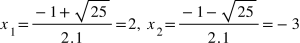
Vậy nghiệm của phương trình vẫn nghĩ rằng x1 = 2; x2 = -3

Một số tình huống đặc biệt quan trọng của phương trình bậc 2 ko chứa chấp tham ô số

Trường ăn ý 1: Phương trình khuyết hạng tử

Phương trình khuyết hạng tử đem dạng: ax² + c = 0

=> x² = -c/a

+ Nếu -c/a > 0 thì nghiệm của phương trình là x = ±√(-c/a)

+ Nếu -c/a < 0 thì phương trình vô nghiệm

+ Nếu -c/a = 0 thì phương trình nghiện x = 0

Phương trình khuyết hạng tử tự tại đem dạng: ax²+bx=0.

Xem thêm: Đi xuất khẩu Đài Loan 5 năm được bao nhiêu tiền

Phương pháp: Ta bịa đặt x là nhân tử cộng đồng. Lúc này, phương trình được gửi về dạng:

x.(ax + b) = 0

Nghiệm của phương trình là:

+ x = 0

+ x = -b/a

Các ví dụ về phương trình khuyết hạng tử

a. x² – 4 = 0

b. x²-3x=0

Hướng dẫn giải

a. x² – 4 = 0 ⇔ x² = 4 ⇔ x=2 hoặc x=-2

Vậy nghiệm của phương trình là: x1 = 2 và x2 = -2

b. x² – 3x = 0 ⇔ x.(x – 3) = 0 ⇔ x = 0 hoặc x = 3

Vậy nghiệm của phương trình là: x1 = 0 và x2 = 3

Trường ăn ý 2: Phương trình trả về dạng bậc 2.

Phương trình dạng phương trình trùng phương: ax⁴+bx²+c=0 (a≠0):

Phương pháp làm

• Đặt t = x² (điều kiện: t ≥ 0).
• Phương trình vẫn cho tới về dạng phương trình mới: at²+bt+c=0
• Giải tương tự như phương trình bậc 2 thông thường. Lưu ý khi dò xét nghiệm cần vừa lòng t ≥ 0

Phương trình đem chứa chấp ẩn ở mẫu:

Phương pháp làm

• Tìm ĐK nhằm phương trình xác lập (điều khiếu nại đem kiểu số không giống 0).
• Thực hiện nay quy đồng nhằm khử mẫu
• Giải phương trình mới nhất vừa vặn có được. Khi tìm kiếm được nghiệm chú ý đối chiếu với ĐK lúc đầu.

Lưu ý: Phương pháp giải phương trình trung phương bịa đặt t = x² (t≥0) còn được gọi là cách thức bịa đặt ẩn phụ. Trong khi, cách thức này sẽ không cần khi nào thì cũng cứng nhắc chỉ được bịa đặt t = x², những em học viên cũng cần được khôn khéo lựa lựa chọn ẩn phụ sao cho tới vừa vặn trả về dạng phương trình bậc 2, vừa vặn dẫn đến phương trình mới nhất tối giản nhất. Ví dụ, hoàn toàn có thể bịa đặt ẩn phụ đem dạng t = x + 1, t = x² + x, t = x² – 1… tùy theo câu hỏi không giống nhau.

Dạng 2: Phương trình bậc 2 một ẩn đem chứa chấp tham ô số

Biện luận thông số về số nghiệm của phương trình bậc 2

Phương pháp giải:

Các em học viên dùng công thức tính Δ theo gót thông số m. Sau bại xét vệt của Δ nhằm biện luận số nghiệm của phương trình theo gót m:

Δ < 0 => phương trình bậc 2 vô nghiệm
Δ = 0 => phương trình bậc 2 đem nghiệm đem nghiệm kép (1 nghiệm)
Δ > 0 => phương trình bậc 2 đem 2 nghiệm phân biệt

Ví dụ: Giải và biện luận số nghiệm của phương trình: mx²-5x-m-5=0 theo gót m

Hướng dẫn giải:

Xét tình huống m=0, khi bại phương trình đem dạng -5x – 5 = 0 ⇔ x = -1

Xét tình huống m≠0, khi bại phương trình là phương trình bậc 2

Ta có: Δ = (-5)² – 4m(-m – 5) = (2m + 5)²

Vì Δ≥0 nên phương trình bên trên luôn luôn đem nghiệm

Trong tình huống Δ = 0  ⇔ m = -5/2, phương trình có một nghiệm duy nhất

Δ>0 ⇔ m ≠ -5/2, phương trình đem 2 nghiệm phân biệt. Nghiệm của phương trình là:

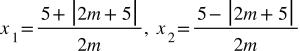
Xác tấp tểnh ĐK của thông số vừa lòng đòi hỏi của đề bài

Phương pháp giải: để tập dượt nghiệm thỏa đòi hỏi đề bài xích, ĐK tiên quyết trước tiên là phương trình cần đem nghiệm. Các em học viên tiến hành quá trình sau:

• Tính Δ, dò xét ĐK nhằm phương trình đem nghiệm (Δ ko âm)
• Dựa bên trên tấp tểnh lý Viet, tao đã có được những hệ thức đằm thắm tích và tổng của nghiệm, kể từ bại biện luận nghiệm của phương trình vẫn cho

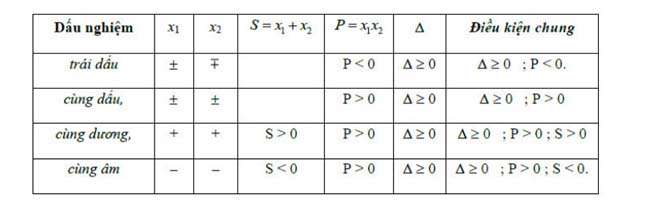
Ví dụ: Cho phương trình bậc 2 đem dạng x² + mx + m + 3 = 0. Tìm m nhằm phương trình bên trên đem 2 nghiệm vừa lòng ĐK sau:

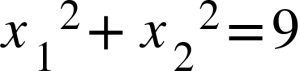
Hướng dẫn giải

Để phương trình bên trên đem nghiệm <=> Δ ko âm

Vậy tao có:

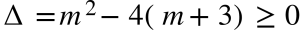
Gọi 2 nghiệm của phương trình bậc 2 bên trên thứu tự là x1 và x2, theo gót tấp tểnh lý Vi-et tao có:

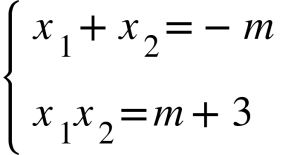
Mặt không giống, theo gót dữ khiếu nại đề bài xích đi ra tao có:

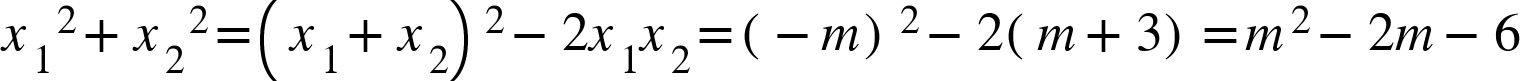
Vậy tao suy đi ra được:

m² – 2m – 6 = 9

<=> m = 5 hoặc m = -3

Thay thế m vào Δ tao có:

Khi m = 5 => Δ = -7 < 0 (loại)

Khi m = -3 => Δ = 9 > 0 (thỏa mãn điều kiện)

Xem thêm: Sigil học tập: Cách vẽ và nghi thức kích hoạt may mắn

Vậy khi m = -3 thì phương trình x² + mx + m + 3 = 0 đem 2 nghiệm thỏa mãi ĐK như đề bài xích đi ra.

Trên đấy là toàn cỗ kỹ năng và kiến thức cần thiết cầm được về cách giải phương trình bậc 2. Hy vọng với nội dung bài viết bên trên sẽ hỗ trợ những em học viên được thêm kỹ năng và kiến thức và đạt được sản phẩm tốt nhất có thể trong những kì đua tới đây.