Diện tích hình tam giác là công thức toán học tập được học tập và vận dụng nhiều trong cả vô cuộc sống. Có thật nhiều công thức và cơ hội vận dụng không giống nhau nhằm tính diện tích S tùy vào cụ thể từng hình tam giác. Bài ghi chép này Trường Cao đẳng Y Khoa Phạm Ngọc Thạch tiếp tục tổ hợp giúp đỡ bạn hiểu rằng những phương pháp tính diện tích S hình tam giác vừa đủ nhất.
1. Tìm hiểu về hình tam giác
1.1. Hình tam giác là hình gì?
Hình tam giác là hình gồm tía đỉnh là tía điểm ko trực tiếp mặt hàng, còn tía cạnh là tía đoạn trực tiếp nối những đỉnh cùng nhau. Đây là hình hai chiều bằng cơ phiên bản vô môn Toán học tập, được xem là một nhiều giác với tối thiểu 3 cạnh. 1 hình tam giác với tổng những góc vô luôn luôn vì như thế 180 chừng.
Bạn đang xem: Công thức tính diện tích hình tam giác và các bài tập cụ thể
>>> Xem thêm Công thức tính chu vi hình tam giác và những bài bác tập dượt minh họa
1.2. Các mô hình tam giác
- Tam giác thường: Đây là 1 tam giác cơ phiên bản nhất vô hình học tập, những cạnh có tính nhiều năm không giống nhau, và số đo những góc cũng không giống nhau. Tam giác thông thường còn bao hàm những tình huống đặc trưng của tam giác.
- Tam giác cân: Tam giác này còn có nhị cạnh cân nhau, còn được gọi là nhị cạnh mặt mũi. Đỉnh của một tam giác cân nặng sẽ là phú điểm so với nhị cạnh mặt mũi. Góc được tạo ra vì như thế 2 cạnh mặt mũi gọi là góc ở đỉnh, góc ở lòng là 2 góc sót lại. Theo đặc thù của tam giác cân nặng thì nhị góc ở lòng cân nhau.
- Tam giác đều: Đây là 1 tình huống đặc trưng của tam giác cân nặng với tía cạnh cân nhau. Theo đặc thù của tam giác đều, 3 góc cân nhau và đều vì như thế 60 chừng.
- Tam giác nhọn: Tam giác này còn có Điểm sáng nhưng mà 3 góc đều nhỏ rộng lớn 90 chừng gọi là tía góc nhọn hoặc toàn bộ góc ngoài đều to hơn 90 chừng gọi là 6 góc tù.
- Tam giác vuông: Là tình huống tam giác với cùng một góc vì như thế 90 chừng, nhị cạnh tạo thành góc vuông thì được gọi là cạnh góc vuông, cạnh sót lại là cạnh huyền.
- Tam giác vuông cân: Vừa là tam giác vuông, vừa phải là tam giác cân nặng.
- Tam giác tù: Đây là tam giác với cùng một góc vô to hơn rộng lớn rộng lớn 90 chừng là 1 trong góc tủ hoặc một góc ngoài bé thêm hơn 90 chừng gọi là 1 góc nhọn.
1.3. Một số đặc thù của hình tam giác
- Số đo 3 góc của một hình tam giác với tổng 180° (định lý tổng tía góc vô của từng tam giác).
- Chiều nhiều năm của từng cạnh thông thường to hơn hiệu chừng nhiều năm nhị cạnh ê và cũng nhỏ rộng lớn đối với tổng chừng nhiều năm của bọn chúng (bất đẳng thức tam giác).
- Trong một tam giác, chiều nhiều năm của cạnh đối lập với góc to hơn tiếp tục to hơn. trái lại, góc đối lập với cạnh to hơn với số đo to hơn (quan hệ thân mật cạnh và góc đối lập vô tam giác).
- 3 đàng cao hạ kể từ 3 đỉnh của một tam giác tách nhau bên trên một điểm gọi là trực tâm của tam giác (đồng quy tam giác).
- 3 đàng trung tuyến của một tam giác tiếp tục tách nhau bên trên một điểm gọi là trọng tâm của tam giác. Từ trọng tâm cho tới cạnh của tam giác với khoảng cách vì như thế 2/3 chừng nhiều năm đàng trung tuyến. Đường trung tuyến của tam giác tiếp tục tạo thành 2 phần với diện tích S cân nhau (đồng quy tam giác).
- 3 đàng trung trực của tam giác phú nhau một điểm gọi là tâm đàng tròn xoe nước ngoài tiếp của tam giác (đồng quy tam giác).
- 3 đàng phân giác của tam giác tách nhau một điểm là tâm đàng tròn xoe nội tiếp của tam giác (đồng quy tam giác).
2. Cách tính diện tích S hình tam giác và bài bác tập dượt cụ thể
2.1. Công thức tính diện tích S tam giác thường
Kiến thức cơ bản:
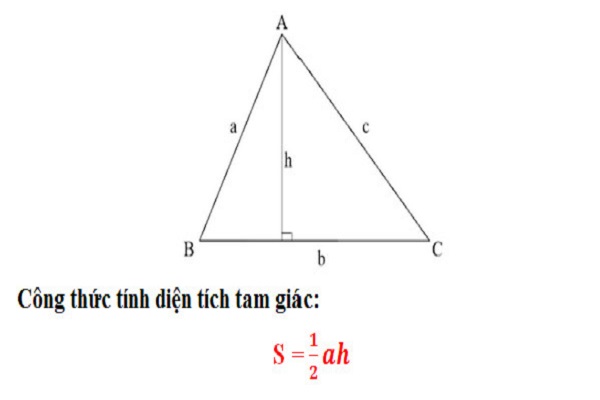
Cách tính Diện tích tam giác thường vì như thế ½ tích của độ cao hạ kể từ đỉnh và chiều nhiều năm cạnh đối lập của tam giác. Nói dễ nắm bắt rộng lớn là chiều nhiều năm cạnh lòng nhân với độ cao rồi phân chia mang đến 2.
Công thức tính diện tích S tam giác thường: S = (a x h) : 2
Trong đó:
- a: Chiều nhiều năm lòng tam giác, vô ê lòng là 1 vô 3 cạnh ngẫu nhiên của tam giác.
- h: Chiều cao của tam giác, ứng với phần lòng chiếu lên. Chiều cao được xem vì như thế đoạn trực tiếp hạ kể từ đỉnh xuống lòng, vuông góc với lòng của một tam giác.
Đây là công thức tính diện tích S hình tam giác cơ phiên bản được vận dụng kể từ lớp 3, 4, 5, 6, 7, 8, 9 cho tới lúc học trung học phổ thông.
Bài tập dượt ví dụ:
Tính diện tích S hình tam giác thông thường khi biết: Độ nhiều năm lòng là 12cm và độ cao là 16cm
Lời giải:
Diện tích của hình tam giác là:
(16 x 12) : 2 = 102 (cm2)
Đáp số: 102cm2
* Chú ý: Trường ăn ý ko cho thấy thêm độ cao và cạnh lòng tam giác thông thường nhưng mà biết trước diện tích S với cạnh sót lại thì vẫn rất có thể vận dụng công thức bên trên nhằm tính.
Kiến thức nâng cao:
Cách tính diện tích S tam giác theo đòi công thức Heron:
Nếu vô tam giác ABC biết chừng nhiều năm 3 cạnh và nửa chu vi P/2 thì diện tích S tam giác theo đòi công thức Heron là
S(ABC) = √(p * (p – a)*(p – b)*(p – c))
Cách tính nửa chu vi Phường vì như thế (a+b+c)/2
Áp dụng lăm le lý Sin:
Nếu vô tam giác ABC biết 1 góc và 2 cạnh thì rất có thể vận dụng lăm le lý Sin nhằm tính diện tích S tam giác như sau:
S(ABC) = (1/2) * a * b * sin(C)
Trong ê, C là góc thân mật của 2 cạnh a, b.
2.2. Công thức tính diện tích S hình tam giác vuông
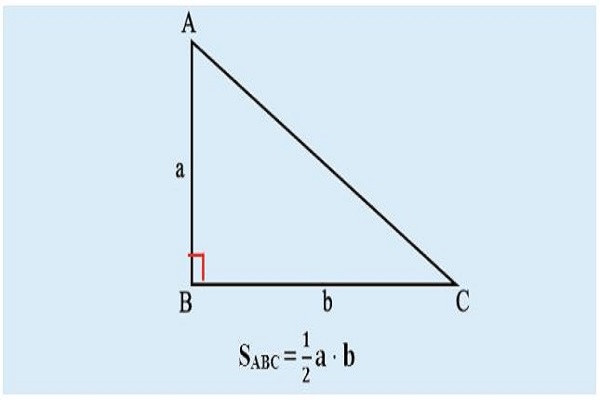
Cách tính Diện tích tam giác vuông vì như thế ½ tích của độ cao là 1 trong vô 2 cạnh góc vuông với cạnh lòng sót lại.
Công thức tính diện tích S tam giác vuông: S = (a x b) / 2
Trong đó: a, b là chừng nhiều năm của nhị cạnh góc vuông.
Tam giác vuông với nhị cạnh góc vuông vì như thế vật độ cao của tam giác tiếp tục ứng với cùng một cạnh góc vuông còn chiều nhiều năm lòng tiếp tục ứng với cạnh góc vuông sót lại.
Điểm khác lạ của tam giác vuông này là hiểu ra được độ cao và chiều nhiều năm cạnh lòng, vậy nên tiếp tục dễ dàng đo lường và tính toán rộng lớn.
Bài tập dượt ví dụ:
Tính diện tích S của tam giác vuông có: Hai cạnh góc vuông thứu tự là 6m và 8m
Lời giải:
Diện tích của hình tam giác vuông là:
(6 x 8) : 2 = 24 (m2)
Đáp số: 24m2
Xem thêm: Cúng đưa ông Táo về trời lúc mấy giờ tốt nhất?
Nếu như việc cho thấy thêm diện tích S và tính chừng nhiều năm thì chúng ta cũng rất có thể người sử dụng công thức bên trên nhằm suy rời khỏi.
Bạn dò thám hiểu thêm thắt về công thức:
- Công thức tính diện tích S, chu vi hình vuông vắn đơn giản
- Công thức tính chu vi và diện tích S hình chữ nhật
2.3. Công thức tính diện tích S hình tam giác cân
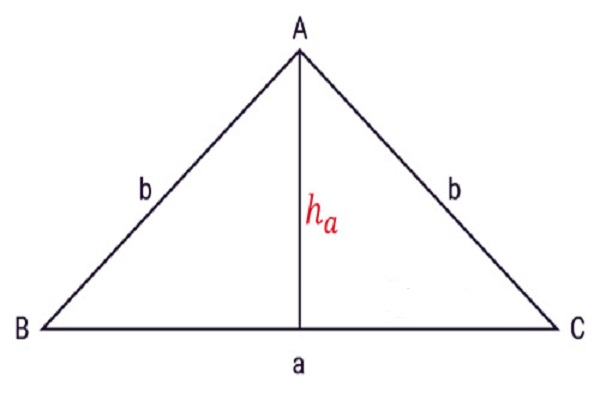
Cách tính diện tích S tam giác cân được xem vì như thế tích của độ cao nối kể từ đỉnh tam giác cho tới cạnh lòng tam giác, rồi phân chia mang đến 2.
Công thức tính diện tích S tam giác cân: S = 50% * (a x h)
- a: Chiều nhiều năm lòng tam giác cân nặng, vô ê lòng là 1 vô 3 cạnh ngẫu nhiên của tam giác.
- h: Chiều cao của tam giác, được xem vì như thế đoạn trực tiếp hạ kể từ đỉnh xuống lòng.
Bài tập dượt ví dụ:
Tính diện tích S của tam giác cân nặng khi biết: Độ nhiều năm cạnh lòng vì như thế 3cm và đàng cao vì như thế 10cm
Lời giải:
Diện tích của hình tam giác là:
(3 x 10) : 2 = 15 (cm2)
Đáp số: 15 cm2
Như phía trên vẫn biết, tam giác cân nặng bao gồm 2 cạnh góc mặt mũi có tính nhiều năm cân nhau và nhị góc cân nhau. Theo ê, phương pháp tính diện tích S tam giác cân nặng tương tự động như tam giác thông thường. quý khách hàng chỉ nên biết về cạnh lòng và độ cao của tam giác cân nặng.
2.4. Công thức tính diện tích S hình tam giác vuông cân
Cách tính tính diện tích S tam giác vuông thăng bằng bình phương chừng nhiều năm cạnh lòng rồi phân chia mang đến 2, vận dụng kể từ công thức tính diện tích S tam giác vuông với độ cao và cạnh lòng cân nhau.
Công thức tính: S = (cạnh đáy)^2/2
- Trong ê, cạnh lòng ko nên là cạnh góc vuông.
2.5. Công thức tính diện tích S hình tam giác đều
Công thức tính diện tích S hình tam giác đều cơ bản:
Cách diện tích S tam giác đều bằng tích của độ cao nối kể từ đỉnh tam giác ê với cạnh lòng tam giác, tiếp sau đó phân chia mang đến 2.
Công thức tính diện tích S tam giác đều: S = (a x h)/ 2
- a: Chiều nhiều năm lòng tam giác đều, vô ê lòng là 1 vô 3 cạnh ngẫu nhiên của tam giác
- h: Chiều cao của tam giác, là đoạn trực tiếp được hạ kể từ đỉnh xuống lòng.
Nếu ko hiểu rằng đàng cao h thì tớ tiếp tục tính độ cao như sau: h = a² – (a/2)² .
Bài tập dượt ví dụ:
Cách tính diện tích S của tam giác khi biết: Độ nhiều năm một cạnh tam giác vì như thế 8cm và đàng cao vì như thế 12cm.
Lời giải:
Diện tích hình tam giác là:
(8 x 12) : 2 = 48 (cm2)
Đáp số: 48cm2
Công thức tính diện tích S tam giác đều theo đòi lăm le lý Heron:
Vì tam giác đều là tam giác với 3 cạnh có tính nhiều năm cân nhau nên diện tích S tam giác đều lăm le lý Heron tiếp tục bằng:
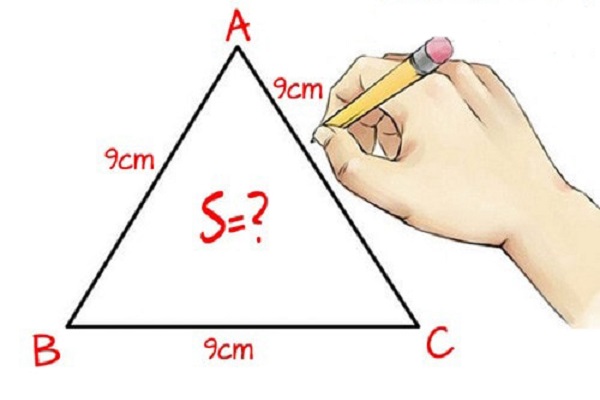
Công thức tính diện tích S tam giác đều theo đòi lăm le lý Cosine:
S(ABC) = (1/2) * a² * sin(60⁰).
Lưu ý: Với ngẫu nhiên công thức tính diện tích S tam giác này thì cũng nên hiểu rằng, ko nên độ cao khi nào thì cũng nằm cạnh vô tam giác, khi ê thì bạn phải vẽ thêm 1 độ cao và cạnh lòng bổ sung cập nhật. Khi ê thì các bạn hãy tính diện tích S tam giác, cần thiết xem xét độ cao nên ứng với cạnh lòng điểm nó chiếu xuống.
2.6. Công thức tính diện tích S tam giác vô không khí Oxyz
Cách tính diện tích S tam giác vô tọa chừng Oxyz vì như thế nửa độ quý hiếm vô cùng của tích hạng tía nhị vectơ AB và AC. Còn được gọi là lăm le thức Determinant.
Công thức tính:
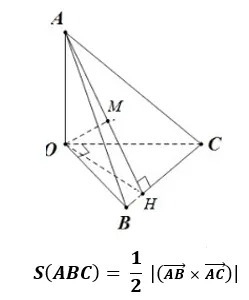
Tam giác vô hệ tọa chừng Oxyz là 1 nhiều giác với 3 cạnh ở trong không khí 3 chiều với ba điểm ko và một đường thẳng liền mạch.
Xem thêm: Cách download Zalo về máy tính, điện thoại nhanh chóng
Xem thêm thắt về những công thức:
- Công thức tính chu vi và diện tích S hình thoi kèm cặp bài bác tập dượt vận dụng
- Công thức tính diện tích S, chu vi hình thang và bài bác tập dượt áp dụng
3. Các dạng bài bác tập dượt phương pháp tính không giống về diện tích S hình tam giác
Ngoài những công thức bên trên, còn tồn tại những công thức tính diện tích S xung xung quanh hình tam giác không giống.
- Cách tính diện tích S hình tam giác lúc biết nửa đường kính đàng tròn xoe nội tiếp: S = (P * r) / 2
- Cách tính diện tích S hình tam giác lúc biết nửa đường kính đàng tròn xoe nước ngoài tiếp: S = (abc) / (4R)
- Công thức tính diện tích S tam giác lúc biết chu vi Phường và nửa đường kính đàng tròn xoe nội tiếp: S = (a*b*c)/(8R)
Bài ghi chép bên trên phía trên Shop chúng tôi vẫn trình diễn công thức tính diện tích S hình tam giác và những dạng bài bác tập dượt giúp đỡ bạn hiểu tính được diện tích S tam giác nhanh gọn, hiệu suất cao nhất. Để biết phương pháp tính nhuần nhuyễn nhất thì các bạn hãy rèn luyện bổ sung cập nhật nhiều bài bác tập dượt không giống nhau. Đừng quên theo đòi dõi nội dung bài viết tiếp theo sau bên trên Trường Cao đẳng Y Khoa Phạm Ngọc Thạch nhằm update kỹ năng và kiến thức tương quan nhé.