nhatkybe
nhatkybe
Trang chủ Uncategorized Công thức lượng giác đầy đủ nhất cho lớp 9, lớp 10, lớp 11

Công thức lượng giác đầy đủ nhất cho lớp 9, lớp 10, lớp 11

Tổng thích hợp những công thức lượng giác vừa đủ nhất sử dụng vô cả lịch trình toán lớp 9, 10, 11, bao hàm những công thức lượng giác cơ phiên bản, công thức nhân, biến hóa tích trở thành cổng, lượng giác của những cung quan trọng đặc biệt, độ quý hiếm lượng giác của những góc quan trọng đặc biệt, những công thức nghiệm cơ phiên bản... Hãy nắm rõ những công thức này nhằm hoàn toàn có thể tổ chức thực hiện những dạng bài bác luyện về lượng giác. Mời chúng ta tìm hiểu thêm.

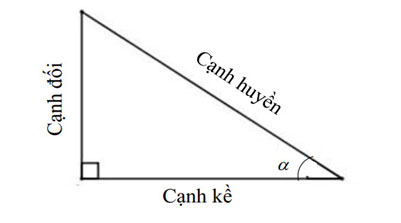
Khái niệm tỉ con số giác của một góc nhọn

Lượng giác

Bạn đang xem: Công thức lượng giác đầy đủ nhất cho lớp 9, lớp 10, lớp 11

Với:

  • sin α: là tỉ số thân thuộc cạnh đối và cạnh huyền của góc α
  • cos α: là tỉ số thân thuộc cạnh kề và cạnh huyền của góc α
  • tan α: là tỉ số thân thuộc cạnh đối và cạnh kề của góc α
  • cot α: là tỉ số thân thuộc cạnh kề và cạnh đối của góc α

Mẹo học tập nằm trong : Sin đến lớp, Cos ko hư hỏng, Tan câu kết, Cot kết đoàn

Công thức quy đổi góc sang trọng radian và ngược lại

Công thức lượng giác cơ bản

1. \tan x =\frac{\sin x}{\cos x}  với x \neq \frac{\pi}{2} + k\pi;\left(k\mathbb{\in Z} \right)

2.\cot x =\frac{\cos x}{\sin x} với x\neq k\pi;\left( k\mathbb{\in Z}\right)

3.\ \sin^2x+\cos^2x=1

4.\ \tan x.\cot x=1\left(x\ne k\frac{\pi}{2},\ k\ ∈\ Z\right)

5.\ 1+\tan^2x=\frac{1}{\cos^2x}\ \left(x\ne\frac{\pi}{2}+k\pi,\ k\ ∈\ Z\right)

6.\ 1+\cot^2x=\frac{1}{\sin^2x}\ \left(x\ne k\pi,\ k\ ∈\ Z\right)

Công thức nằm trong lượng giác

1. sin (a ± b) = sin a.cos b ± cos a.sin b

2. cos (a + b) = cos a.cos b - sin a.sin b

3. cos (a - b) = cos a.cos b + sin a.sin b

4.\ \tan\left(a+b\right)=\frac{\tan a+\tan b}{1-\tan.\tan b}

5.\ \tan\left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a.\tan b}

Mẹo ghi nhớ công thức cộng: Sin thì sin cos cos sin, cos thì cos cos sin sin vệt trừ. Tan thì tan nọ tan bại liệt phân chia mang lại kiểu số 1 trừ tan tan.

Công thức những cung link bên trên đàng tròn xoe lượng giác

Mẹo nhớ: cos đối, sin bù, phụ chéo cánh, tan rộng lớn thông thường π

Với từng góc lượng giác α và số vẹn toàn k tao có:

Hai góc đối nhau:

  • cos (-x) = cos x
  • sin (-x) = -sin x
  • tan (-x) = -tan x
  • cot (-x) = -cot x

Hai góc bù nhau:

  • sin (π - x) = sin x
  • cos (π - x) = -cos x
  • tan (π - x) = -tan x
  • cot (π - x) = -cot x

Hai góc phụ nhau:

  • sin (π/2 - x) = cos x
  • cos (π/2 - x) = sin x
  • tan (π/2 - x) = cot x
  • cot (π/2 - x) = tan x

Hai góc rộng lớn thông thường π:

  • sin (π + x) = -sin x
  • cos (π + x) = -cos x
  • tan (π + x) = tan x
  • cot (π + x) = cot x

Hai góc rộng lớn thông thường π/2:

  • sin (π/2 + x) = cos x
  • cos (π/2 + x) = -sin x
  • tan (π/2 + x) = -cot x
  • cot (π/2 + x) = -tan x

Công thức nhân đôi

Công thức nhân đôi

Công thức nhân ba

Công thức nhân bốn

  • sin4a = 4.sina.cos3a - 4.cosa.sin3a
  • cos4a = 8.cos4a - 8.cos2a + 1 hoặc cos4a = 8.sin4a - 8.sin2a + 1

Công thức hạ bậc

Thực đi ra những công thức này đều được biến hóa đi ra kể từ công thức lượng giác cơ phiên bản, ví dụ như: sin2a=1 - cos2a = 1 - (cos2a + 1)/2 = (1 - cos2a)/2.

1.\ \sin^2a\ =\ \frac{1-\cos2a}{2}

2.\ \cos^2a=\frac{1+\cos2a}{2}

3.\ \sin^3a=\frac{3\sin a-\sin3a}{4}

4.\ \cos^3a=\frac{3\cos a+\cos3a}{4}

Công thức biến hóa tổng trở thành tích

Mẹo nhớ: cos nằm trong cos vì thế 2 cos cos, cos trừ cos vì thế trừ 2 sin sin; sin nằm trong sin vì thế 2 sin cos, sin trừ sin vì thế 2 cos sin.

Xem thêm: Nguyễn Ái Quốc và lớp huấn luyện chính trị ở Quảng Châu

1.\ \cos a+\cos b=2\cos\frac{a+b}{2}.\cos\frac{a-b}{2}

2.\ \cos a-\cos b=-2\sin\frac{a+b}{2}.\sin\frac{a-b}{2}

3.\ \sin\ a+\sin b=2\sin\frac{a+b}{2}.\cos\frac{a-b}{2}

4.\ \sin\ a-\sin b=2\cos\frac{a+b}{2}.\sin\frac{a-b}{2}

5.\ \tan a+\tan b=\frac{\sin\left(a+b\right)}{\cos a.\cos b}

6.\ \tan a-\tan b=\frac{\sin\left(a-b\right)}{\cos a.\cos b}

7.\cot a + \cot b = \frac{\sin(a +b)}{\sin a.\sin b}

8.\cot a - \cot b = - \frac{\sin(a -b)}{\sin a.\sin b}

9.\ \sin a+\cos a=\sqrt{2}\sin\left(a+\frac{\pi}{4}\right)=\sqrt{2}\cos\left(a-\frac{\pi}{4}\right)

10.\ \sin a-\cos a=\sqrt{2}\sin\left(x-\frac{\pi}{4}\right)=-\sqrt{2}\cos\left(x+\frac{\pi}{4}\right)

11.\ \tan a+\cot a=\frac{2}{\sin2a}

12.\ \cot a-\tan a=2\cot2a

13.\ \sin^4a+\cos^4a=1-\frac{1}{2}\sin^22a=\frac{1}{4}\cos4a+\frac{3}{4}

14.\ \sin^6a+\cos^6a=1-\frac{3}{4}\sin^22a=\frac{3}{8}\cos4a+\frac{5}{8}

Công thức biến hóa tích trở thành tổng

1.\ \cos a.\cos b=\frac{1}{2}\left[\cos\left(a+b\right)+\cos\left(a-b\right)\right]2.\ \sin a.\sin b=-\frac{1}{2}\left[\cos\left(a+b\right)-\cos\left(a-b\right)\right]

3.\ \sin a.\cos b=-\frac{1}{2}\left[\sin\left(a+b\right)+\sin\left(a-b\right)\right]

Phương trình lượng giác

Phương trình lượng giác cơ bản

1.\sin a = \sin b \Leftrightarrow \left[ \begin{gathered} a = b + k2\pi \hfill \\ a = \pi - {\text{b}} + {\text{k}}2\pi \hfill \\ \end{gathered} \right.\left( {k \in \mathbb{Z}} \right)

2.\cos a = \cos b \Leftrightarrow \left[ \begin{gathered} a = b + k2\pi \hfill \\ a = - b + k2\pi \hfill \\ \end{gathered} \right.\left( {k \in \mathbb{Z}} \right)

3. tan a = tan b ⇔ a = b + kπ; (k ∈ Z)

4. cot a = cot b ⇔ a = b + kπ; (k ∈ Z)

Phương trình lượng giác quánh biệt

Dấu của những độ quý hiếm lượng giác

Góc phần tư sốIIIIIIIV
Giá trị lượng giác
sin x++--
cos x+--+
tan x+-+-
cot x+-+-

Bảng độ quý hiếm lượng giác một số trong những góc quánh biệt

Bảng độ quý hiếm lượng giác một số trong những góc quánh biệt

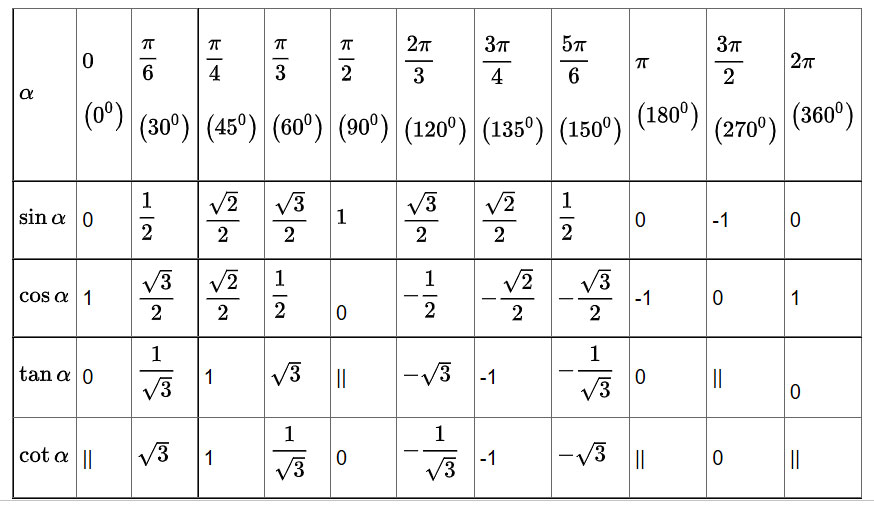
Quan sát trực quan lại những góc quan trọng đặc biệt bên trên đàng tròn xoe lượng giác như sau:

Công thức lượng giác vừa đủ nhất mang lại lớp 9, lớp 10, lớp 11

Tỉ con số giác của 2 góc phụ nhau. (α + β = 90°)

sin α = cos βcos α = sin β
tan α = cot β

cot α = tan β

Công thức lượng giác té sung

Biểu thao diễn công thức theo đuổi t=\frac{\tan a}{2}  

Xem thêm: Tranh vẽ anime của Trí tuệ nhân tạo khiến netizen bất ngờ vì 1 điều

1.\ \sin a=\frac{2t}{1+t^2}\ \ \ \ \ \ \ \ \ \ \ \ 2.\ \cos a=\frac{1-t^2}{1+t^2}

3.\ \tan\ a=\frac{2t}{1-t^2}\ \ \ \ \ \ \ \ \ \ 4.\ \cot a=\frac{1-t^2}{2t}

Các công thức đạo hàm và đạo nồng độ giác vừa đủ nhất

BÀI VIẾT NỔI BẬT

Cách Cách Vẽ Xe Máy Độ với những mẫu xe độ đa dạng

Chủ đề: Cách Vẽ Xe Máy Độ Cách Vẽ Xe Máy Độ: Vẽ xe máy độ là một trong những bức tranh nghệ thuật thú vị, đặc biệt là đối với những người yêu thích các chiếc xe độ. Tìm kiếm trên mạng hướng dẫn vẽ xe máy độ và thực hành kỹ năng của mình. Bạn cũng có thể tham khảo các mẫu vẽ để tạo ra những bức tranh nghệ thuật độc đáo. Chú ý đến chi tiết và sử dụng màu sắc một cách hợp lý để tạo ra những tác phẩm nghệ thuật tuyệt vời.

Quy định hoàn đổi vé của Vietjet Air

Sau khi đã đặt mua vé bay của Hãng hàng không Vietjet Air, nhưng vì một lý do nào đó bắt buộc quý khách phải thay đổi hoặc hoàn vé với dự định ban đầu, hãy ...